What Is A Consecutive Angle? A Comprehensive Guide To Unlocking The Mystery

Karina Strosin 13 May 2025

Alright, let’s dive right into it. If you’ve ever been scratching your head over geometry terms like “consecutive angles,” you’re not alone. Whether you’re a student cramming for a test or just someone curious about math, understanding what consecutive angles are is simpler than it sounds. So buckle up, because we’re about to demystify this concept in a way that’ll make you say, “Oh, that’s all it is?”

Consecutive angles pop up in geometry more often than you might think, and they’re actually pretty cool once you get the hang of them. Think of them as BFFs in the world of shapes—angles that hang out together and share some interesting properties. In this article, we’re gonna break down everything you need to know about consecutive angles, from the basics to the more advanced stuff.

But before we get too deep, let’s address the elephant in the room. If you’re here, chances are you’ve got questions. Maybe you’re wondering, “Are consecutive angles the same as adjacent angles?” or “Do they only exist in parallelograms?” Don’t worry, we’ll cover all that and more. So grab a snack, sit back, and let’s unravel the mystery of consecutive angles together.

Understanding the Basics of Consecutive Angles

First things first, what exactly is a consecutive angle? Simply put, consecutive angles are angles that follow one another in sequence. They’re like best friends who stick together, often sharing a side or vertex in certain geometric shapes. To break it down further, consecutive angles are typically found in polygons, where they are adjacent to each other and share a common side.

For example, in a parallelogram, consecutive angles are the ones that are next to each other. If you label the angles as A, B, C, and D, then A and B are consecutive, as are B and C, C and D, and D and A. It’s like a circle of friendship where everyone knows their neighbor.

Consecutive Angles vs. Adjacent Angles: What’s the Difference?

Now, here’s where things can get a little tricky. Many people confuse consecutive angles with adjacent angles, but they’re not exactly the same thing. While both types of angles share a side, consecutive angles specifically refer to angles that follow each other in a sequence within a polygon. Adjacent angles, on the other hand, are any two angles that share a common vertex and side, regardless of their position in the shape.

Think of it this way: all consecutive angles are adjacent, but not all adjacent angles are consecutive. For instance, in a triangle, you have three adjacent angles, but since there’s no sequence, you wouldn’t call them consecutive. Got it? Good. Let’s move on.

Key Characteristics of Consecutive Angles

They are always next to each other in a polygon.
They share a common side.
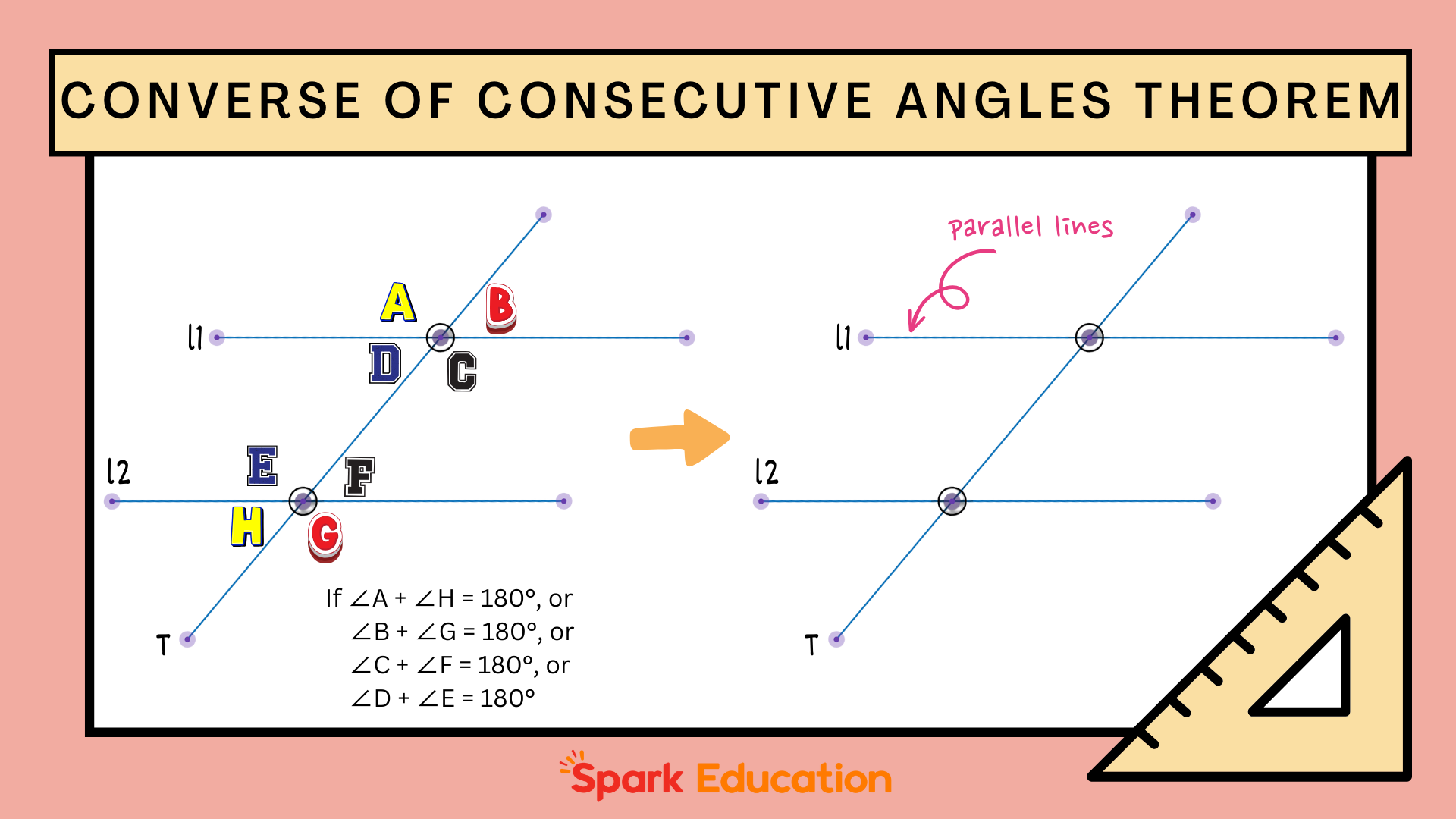
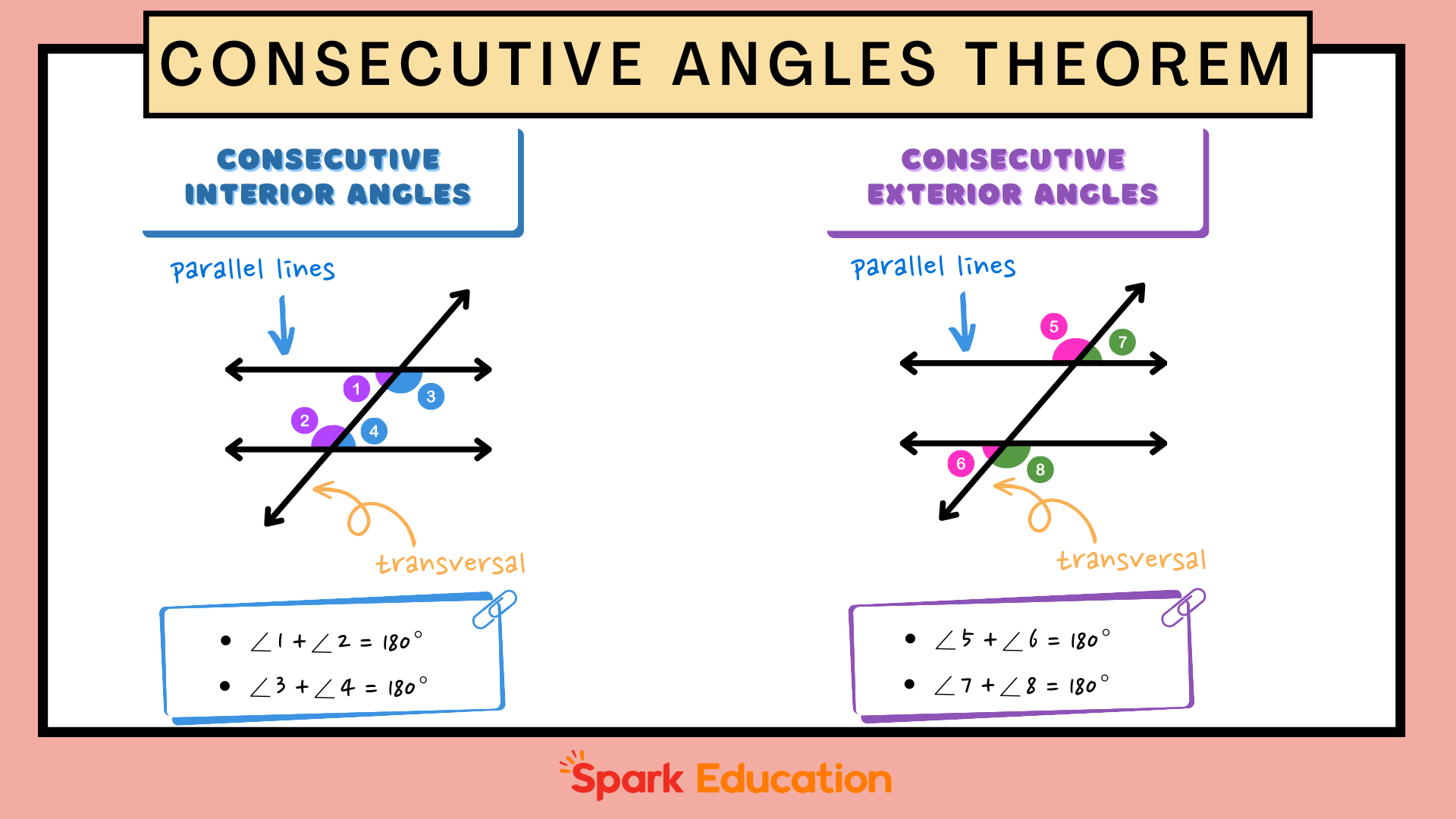
They are supplementary in parallelograms (meaning their sum is 180 degrees).
They can exist in any polygon with more than three sides.

Where Do Consecutive Angles Show Up?

Consecutive angles aren’t just theoretical concepts—they show up in real-life situations too! For instance, if you’re designing a building or working on a blueprint, understanding consecutive angles can help you ensure that everything lines up perfectly. They’re also crucial in fields like engineering, architecture, and even art, where precision matters.

In addition, consecutive angles play a big role in geometry problems. Whether you’re calculating the angles of a quadrilateral or trying to figure out the missing piece of a puzzle, knowing how consecutive angles work can save you a lot of time and headaches.

Examples of Consecutive Angles in Real Life

The corners of a picture frame.
The angles formed by the sides of a stop sign.
The angles in a kite or a diamond-shaped object.

How to Identify Consecutive Angles in a Polygon

Identifying consecutive angles in a polygon is easier than it seems. All you need to do is look for angles that are next to each other and share a common side. For example, in a rectangle, the top-left angle and the top-right angle are consecutive because they share the top side. The same goes for the bottom-left and bottom-right angles.

Here’s a quick tip: if you’re working with a parallelogram, remember that consecutive angles are always supplementary. That means if one angle is 120 degrees, the angle next to it will be 60 degrees. It’s like a balancing act where the two angles work together to add up to 180 degrees.

Step-by-Step Guide to Finding Consecutive Angles

Identify the vertices of the polygon.
Look for angles that share a common side.
Check if the angles are next to each other in sequence.
Verify if they are supplementary (if applicable).

Consecutive Angles in Special Quadrilaterals

Quadrilaterals are where consecutive angles really shine. In shapes like parallelograms, rectangles, and rhombuses, consecutive angles have some unique properties that make them stand out. For instance, in a parallelogram, consecutive angles are always supplementary, meaning they add up to 180 degrees. In a rectangle, all consecutive angles are 90 degrees, making it a perfect example of symmetry.

Rhombuses also have their own set of rules. While opposite angles are equal, consecutive angles are supplementary, just like in a parallelogram. It’s like a game of angles where each shape has its own set of rules to follow.

Properties of Consecutive Angles in Parallelograms

They are supplementary.
They share a common side.
They are always next to each other.

The Math Behind Consecutive Angles

Now, let’s get a little more technical. Mathematically speaking, consecutive angles are defined by their position in a polygon and their relationship to each other. In a parallelogram, for example, if angle A is x degrees, then angle B (its consecutive angle) will be 180 - x degrees. This relationship holds true for all consecutive angles in a parallelogram.

In a regular polygon, where all sides and angles are equal, consecutive angles are simply the angles that follow each other in sequence. For example, in a regular hexagon, each angle is 120 degrees, and consecutive angles are simply the ones that come after each other in the sequence.

Formula for Calculating Consecutive Angles

If you’re dealing with a parallelogram, the formula for consecutive angles is simple:

Angle 1 + Angle 2 = 180 degrees

For regular polygons, the formula for each angle is:

(n - 2) × 180 / n

Where n is the number of sides in the polygon.

Common Mistakes to Avoid When Working with Consecutive Angles

Even the best mathematicians make mistakes sometimes, and consecutive angles are no exception. One common mistake is confusing consecutive angles with adjacent angles, as we mentioned earlier. Another mistake is forgetting that consecutive angles in a parallelogram are supplementary. Always double-check your work to make sure you’re applying the right rules.

Another pitfall is assuming that all consecutive angles are supplementary. While this is true for parallelograms, it’s not always the case for other polygons. Always check the specific properties of the shape you’re working with.

Tips for Avoiding Errors

Double-check the definition of consecutive angles.
Verify if the angles are supplementary (if applicable).
Use diagrams to visualize the angles.

Conclusion: Why Consecutive Angles Matter

So there you have it—a comprehensive guide to understanding consecutive angles. From their basic definition to their applications in real life, we’ve covered everything you need to know. Whether you’re a geometry enthusiast or just someone trying to pass a math test, consecutive angles are an important concept to master.

Remember, consecutive angles aren’t just about numbers and formulas—they’re about relationships. They teach us how shapes work together and how angles interact with each other. So the next time you see a polygon, take a closer look at its angles. You might just discover something new!

Now it’s your turn. Did this article help you understand consecutive angles better? Leave a comment below and let me know. And if you found this helpful, don’t forget to share it with your friends. Who knows? You might just turn them into geometry fans too!

Understanding the Basics of Consecutive Angles
Consecutive Angles vs. Adjacent Angles: What’s the Difference?
Where Do Consecutive Angles Show Up?
How to Identify Consecutive Angles in a Polygon
Consecutive Angles in Special Quadrilaterals
The Math Behind Consecutive Angles
Common Mistakes to Avoid When Working with Consecutive Angles
Conclusion: Why Consecutive Angles Matter

PPT Angles and Parallel Lines PowerPoint Presentation, free download

A Complete Guide to Consecutive Angles in Geometry

Spotlight Scroll News